a) reading data and checking sizes
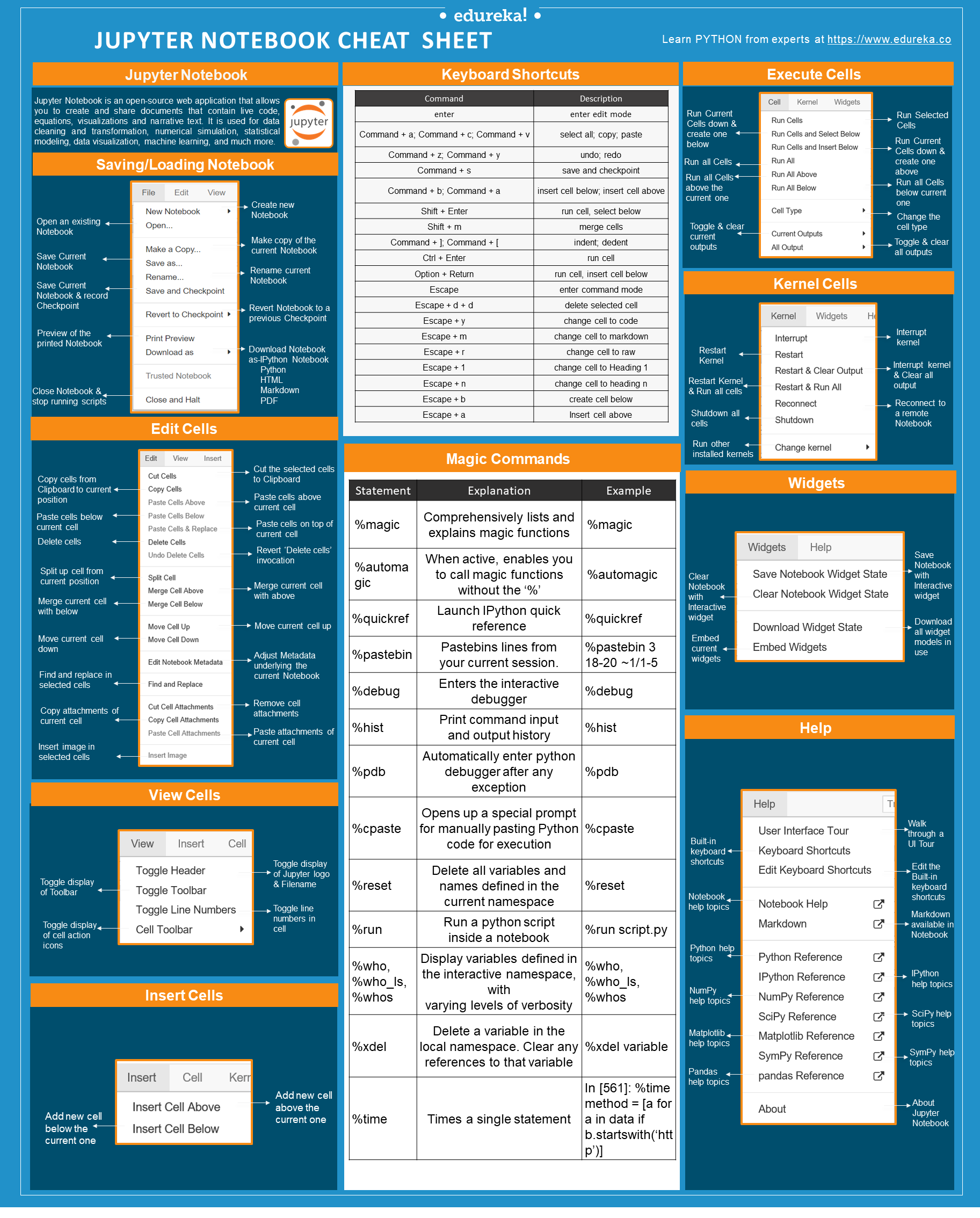
Jupyter notebooks are made up of cells, which can either contain code or Markdown text. Markdown is a simple “language” that allows you to include formatting instructions directly in the text — bold, italics, headers, links, images, code, and more. What is Jupyter Notebook? A Jupyter notebook is a web application that allows the user to write codes and rich text elements. Inside the Notebooks, you can write paragraph, equations, title, add links. Includes Markdown and IpyWidgets!! Guide to the Install Jupyter Notebook. Here we discuss Installation Jupyter Notebook in two Different ways, and its Features.
- We have correct spacing, 0.5 mm
- y represents the whole diameter of the tube
- the shapes are right, i.e the rows and columns have correct sizes
b) contour of velocity field
conclusions
- the water velocity is significantly lower than air velocity
- water velocity is higher at the left part of the image
- lower parts of the water are almost not moving
- one can almost observe the interface between water and air, solely from the velocity distribution
c) quiver and rectangles plot
d) divergence of vector field
divergence is the flux into a volume
The gas is incompressible, for the divergence, this means that its absolute value has to be zero
The sum of the acceleration for the u and v components are thus the negative of the acceleration in the w component. The reason that the code does not compute the real divergence is because we do not take the w-component into account
above I use the gradient operator to solve the problem:
The components of the above equations contains what we need to compute the divergence.
Jupyter Notebook Shortcut Markdown Cell
conclusions
- the divergence is high in the middle, that makes sense, since a wavefront is rushing towards the area
- other areas has low divergence, not much net volume rusing into area
- from the plot, one can conclude that the fluids are incompressible under the current environment
e) curl z-component
to get the component of curl normal to the xy-plane:
$gamma$ contains a list of the list containing the partial derivatives for each component.
The difference of the second from the first gives us the result we want.
We have the necessary variables dvdx and dudy from the previous exercise
conclusions
main take-away is again that there is something intersting happening where the wavefront is headed.

to take the curve integral, we can do the following $int_lambda vec{v} cdot dvec{r}$
since we have a constant spacing in the grid of 5mm, we can calculate the curve integral for each side numerically as follows:
where $x_i$ is the points in the rectangle grid in x-direction, and $x_0$ and $x_1$ etc. are constant levels that are not changing because we are doing summations vertically or horizontally in the grid, thus either x or y is constant.
Jupyter Notebook Shortcut To Markdown
stokes theorem tells us that there is a relation between the line integral and the area-integral:
$int_lambda vec{v} cdot dvec{r} = int_sigma nabla times vec{v} cdot vec{n} quad dsigma$
where $times$ is the cross product operator:
and $nabla$ is:
Our area is $0.25mm^2$, since the cells in the grid are squares with $s=0.5$
we have the z-component of the curl from previous exercise. The curl is different for each cell in our grid.
calculation is done with a sum as the direct calculation over
conclusions
- There is greater circulation around the middle rectangle, which is consistent with the velocity field
- the high z-components of the curl in previous exercises hinted to high circulation around middle area. Confirmed.
- low circulations around other rectangles as expected
g ) Gauss’s theorm
calculation of flux through the sides of the rectangle is similar numerically to the circulation, only that u and v are interchanged for each side. example: the flux through r2(green) is decided by u and not v like in the circulation calculation

gauss theorem is a relation between area and volume integrals
numerically, the calculation is similar to the above examples.
conclusions
- high flux into middle rectangle makes sense, since the wavefront is heading into the area.
